Formal Grammer(형식 언어)

전공 지식 - 인공지능

Language

언어라는 대상을 추상화하여 모델을 만든다. 기호를 부여하고, 연산을 정의하여 대수적(기계적)으로 처리할 수 있게 된다.

알파벳

하나 이상의 symbol(특정 언어에서 사용하는 문자, 기호)들의 유한집합. 기호 𝚺로 표현한다.

문자열(string)

주어진 알파벳에 속한 symbol들의 유한 길이 순열이다.

• 𝚺⁺: 𝚺*에서 𝞴(길이가 0인 문자열, 𝜺으로 표현하기도 한다)를 제외한 집합
• 𝚺*: 𝚺에 포함된 symbol들을 0개 이상 연결(concat)하여 만든 string 집합
• 𝜶, 𝜷, 𝜸, … 등의 그리스 문자는 string을 의미한다.

언어는 일반적으로 𝚺*의 부분집합이다. 임의의 언어 𝐋에 포함되는 string을 언어𝐋의 sentence라고 한다.

Grammer

특정 언어의 문법 G는 다음과 같은 qaurdruple로 정의된다. G = (V, T, P, S)

• V(VN): Non-terminal symbol들의 유한집합. Production rule에 의해 group of terminal symbol로 대체될 수 있다.
• T(VT): Terminal symbol들의 유한집합
• P: Production rules(생성규칙)의 유한집합. Grammer의 핵심이다.
  ex) 𝞪→𝞫, 𝞪∈V⁺, 𝞫∈V\* : 𝞪는 𝞫로 대체될 수 있다는 규칙
• S: Start variable. V의 원소로, 특별한 symbol이다.

V와 T는 서로소라고 가정하고 둘을 합쳐서 Vocabulary라고 한다.

예제

Derivation (유도)

=> 기호를 사용하여 표현한다. 정의된 문법으로부터 어떤 언어가 생성되는지, 언어가 문법에 맞는지를 확인할 수 있다. -> 기호는 생성 규칙을 표현한다.

Formal Grammer (형식문법)

형식 언어는 주어진 알파벳으로 주어진 규칙을 따라 생성된 단어(word, 의미를 가지는 string)로 구성된다.
Formal grammer란 특정 형식 언어에 포함되는 string(word)을 생성하는데 사용되는 유한 개의 생성 규칙(production rule) 집합을 말한다.

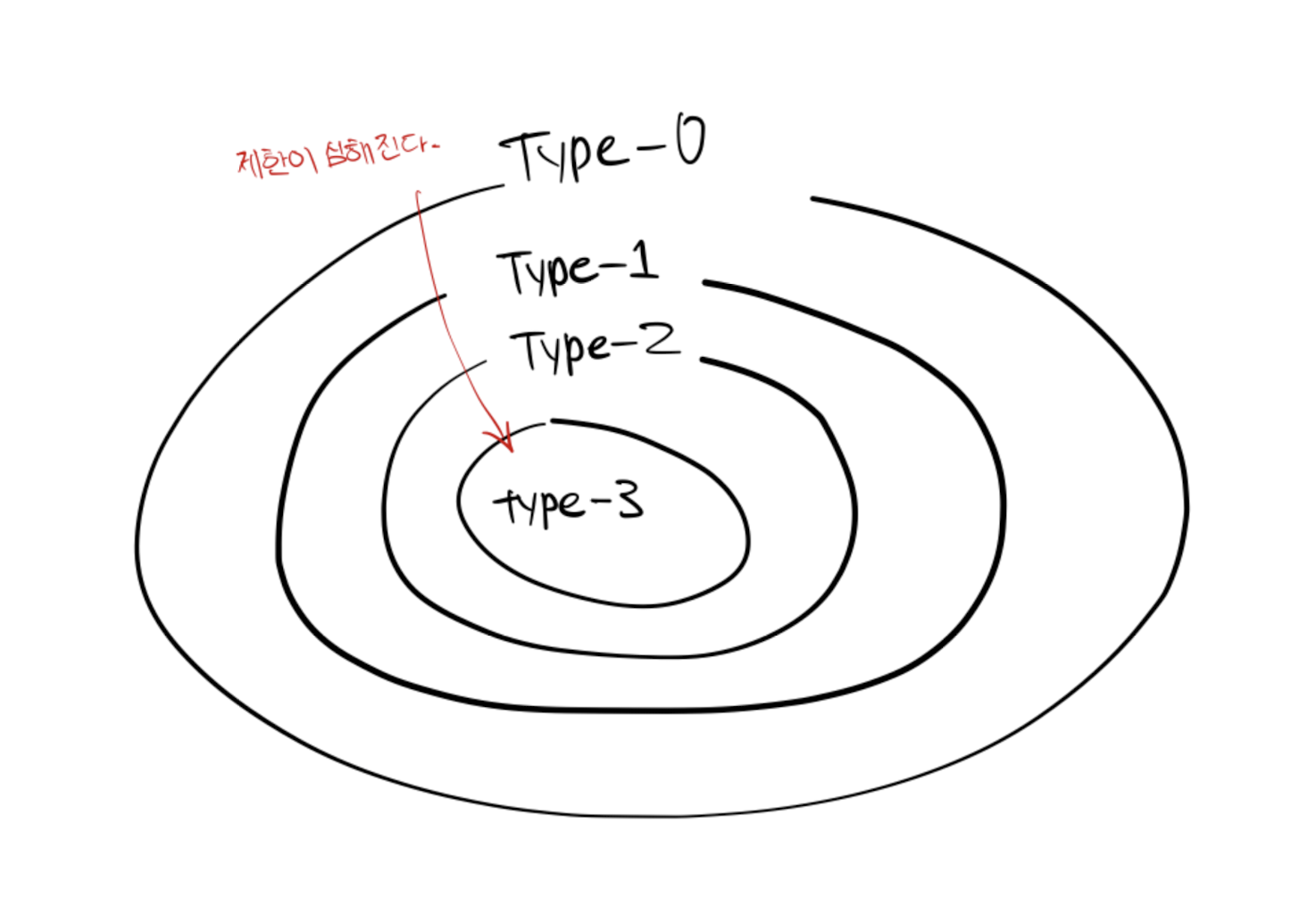
Avram Noam Chomsky는 형식문법을 생성규칙의 형태에 가해지는 제한에 따라 네 가지로 분류했다.

• Type-3 (정규 문법)
• Type-2 (문맥 자유 문법) - 대부분의 프로그래밍 언어 문법의 기초
• Type-1 (문맥 의존 문법)
• Type-0 (무제약 문법) - 모든 형식문법을 포함한다. 튜링 기계로 인식 가능한 모든 언어를 생성한다.

Type-3 grammer

정규문법(regular grammer)이라고도 한다. 생성규칙에 따라 두 종류가 존재한다.
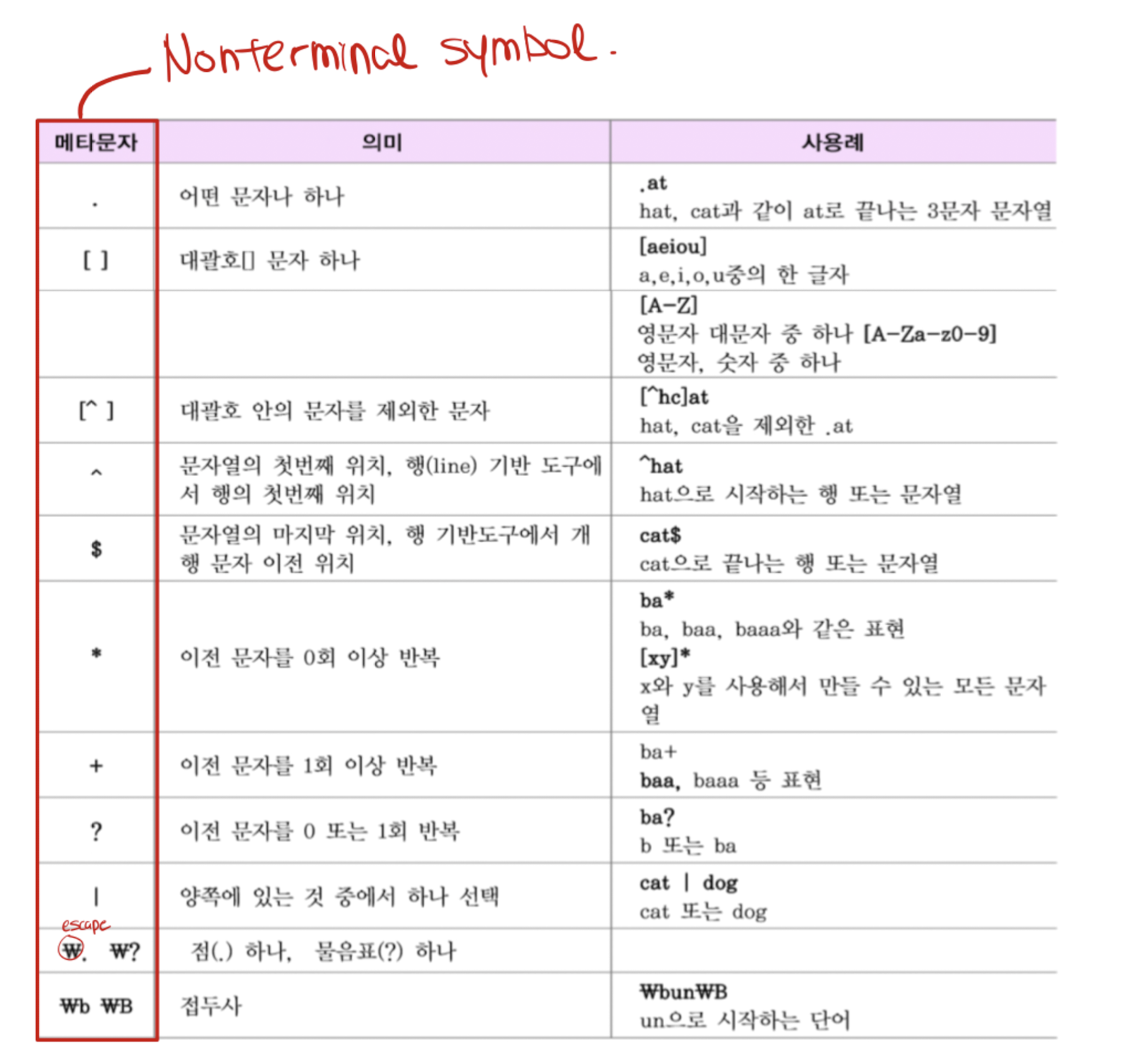
정규문법에 의해 생성되는 언어를 정규 언어라고 한다. **정규식(regular expression)으로 표현이 가능하다.

• 우선형(right linear) 문법 - A->tB, A->t, A->𝜺
• 좌선형(left linear) 문법 - A->Bt, A->t, A->𝜺

하나의 non-terminal symbol은 반드시 하나의 terminal symbol 또는 𝜺 또는 terminal+non-terminal(concat) 중 하나로 대체되어야 한다.

reference

• 3-2 인공지능 강의 필기노트
• 인공지능 튜링 테스트에서 딥러닝까지