Transformation

컴퓨터 그래픽스 - Transformation

Linear transformation

벡터공간에서의 벡터공간으로의 함수(대응)을 transformation 또는 map이라고 한다. Transformation T가 임의의 벡터 𝐮와 𝐯, 임의의 스칼라 𝓀에 대해 다음을 만족하면 linear transformation이라고 한다.

• T(𝐮+𝐯) = T(𝐮) + T(𝐯) : T preserves vector eddition
• T(𝓀𝐮) = 𝓀T(𝐮) : T preserves scalar multiplication

모든 선형변환은 행렬의 곱으로 표현할수 있고 행렬의 곱은 컴퓨터로 계산이 가능하다.

2D Tranformation

rotation

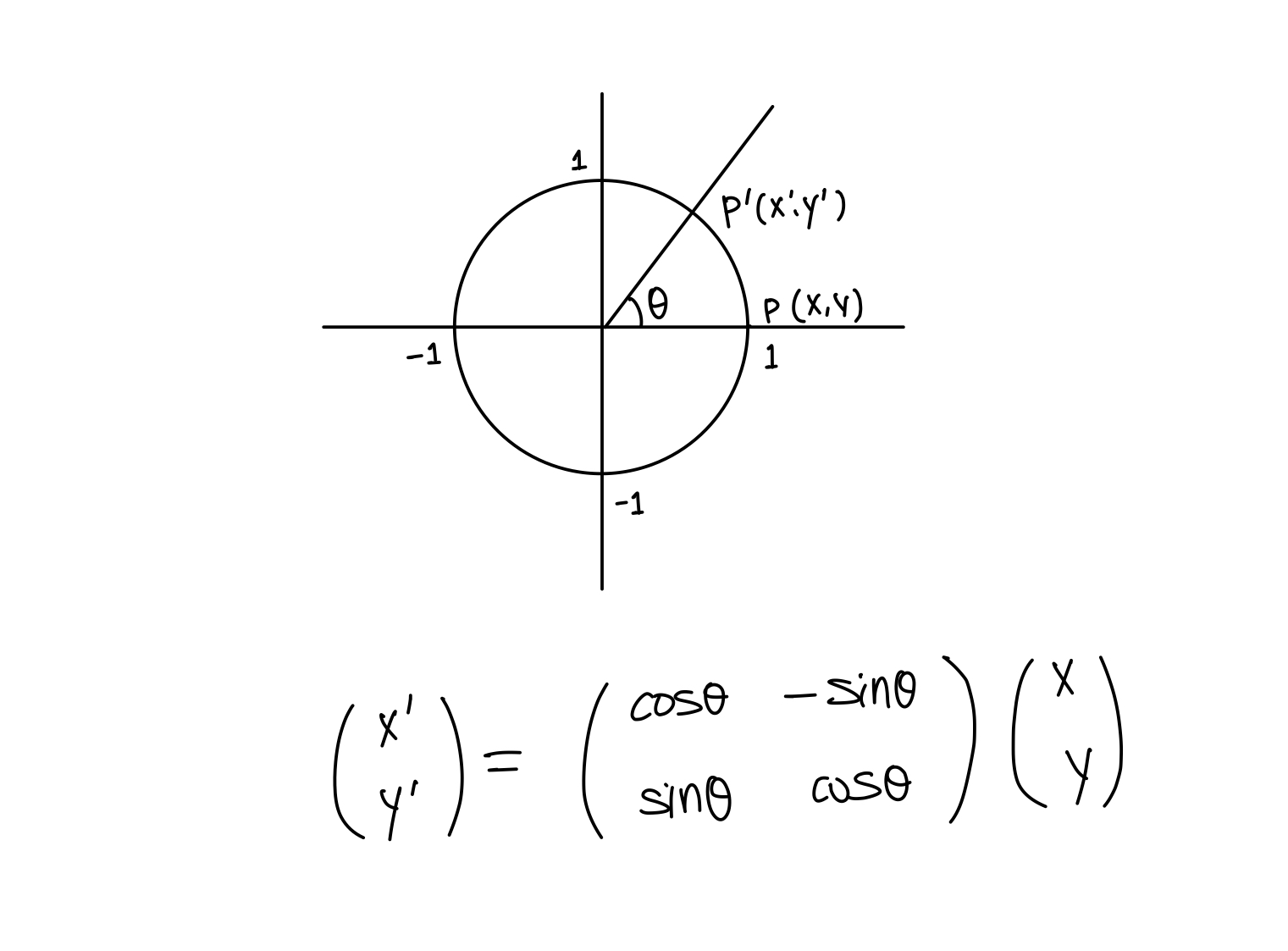
scaling

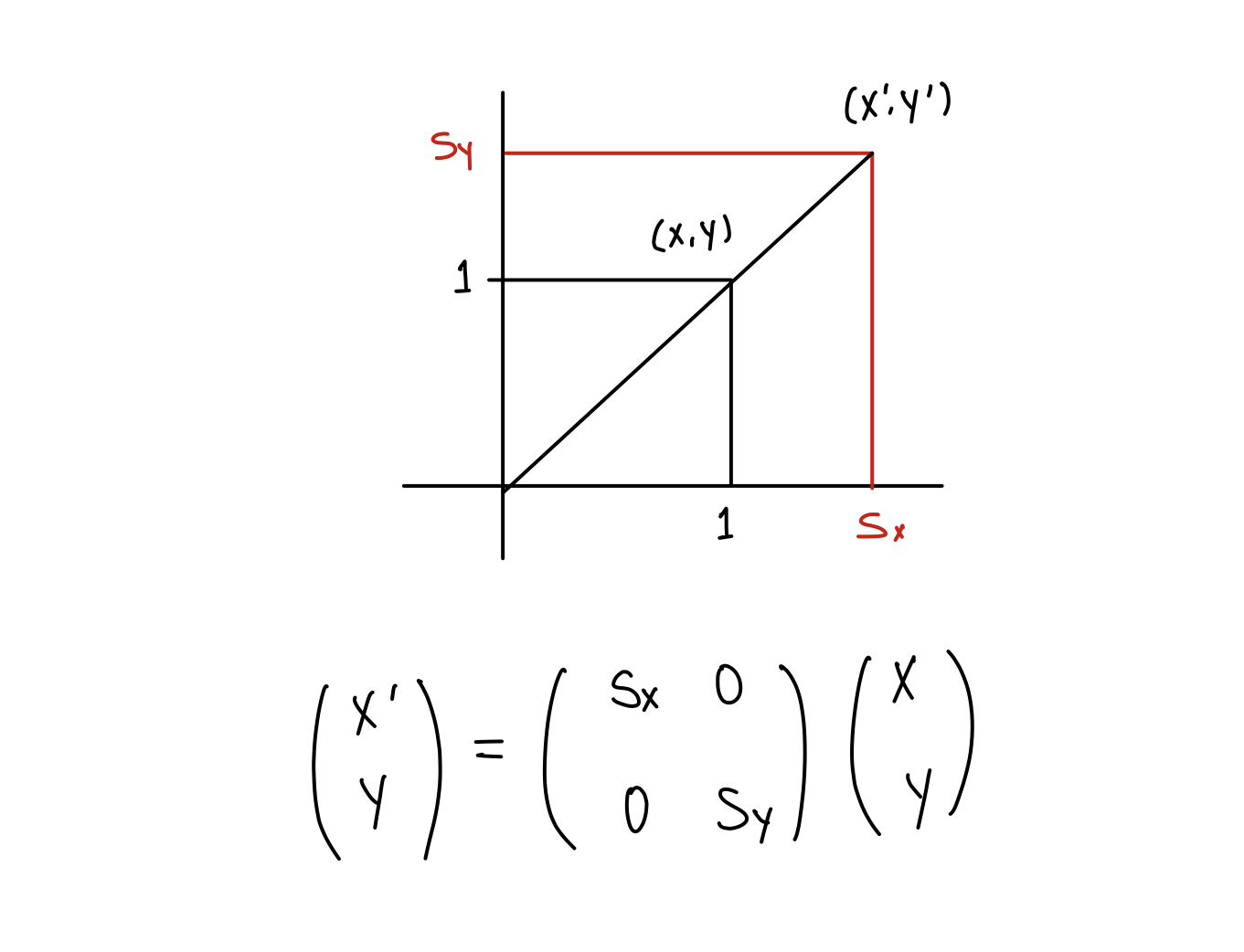
shearing

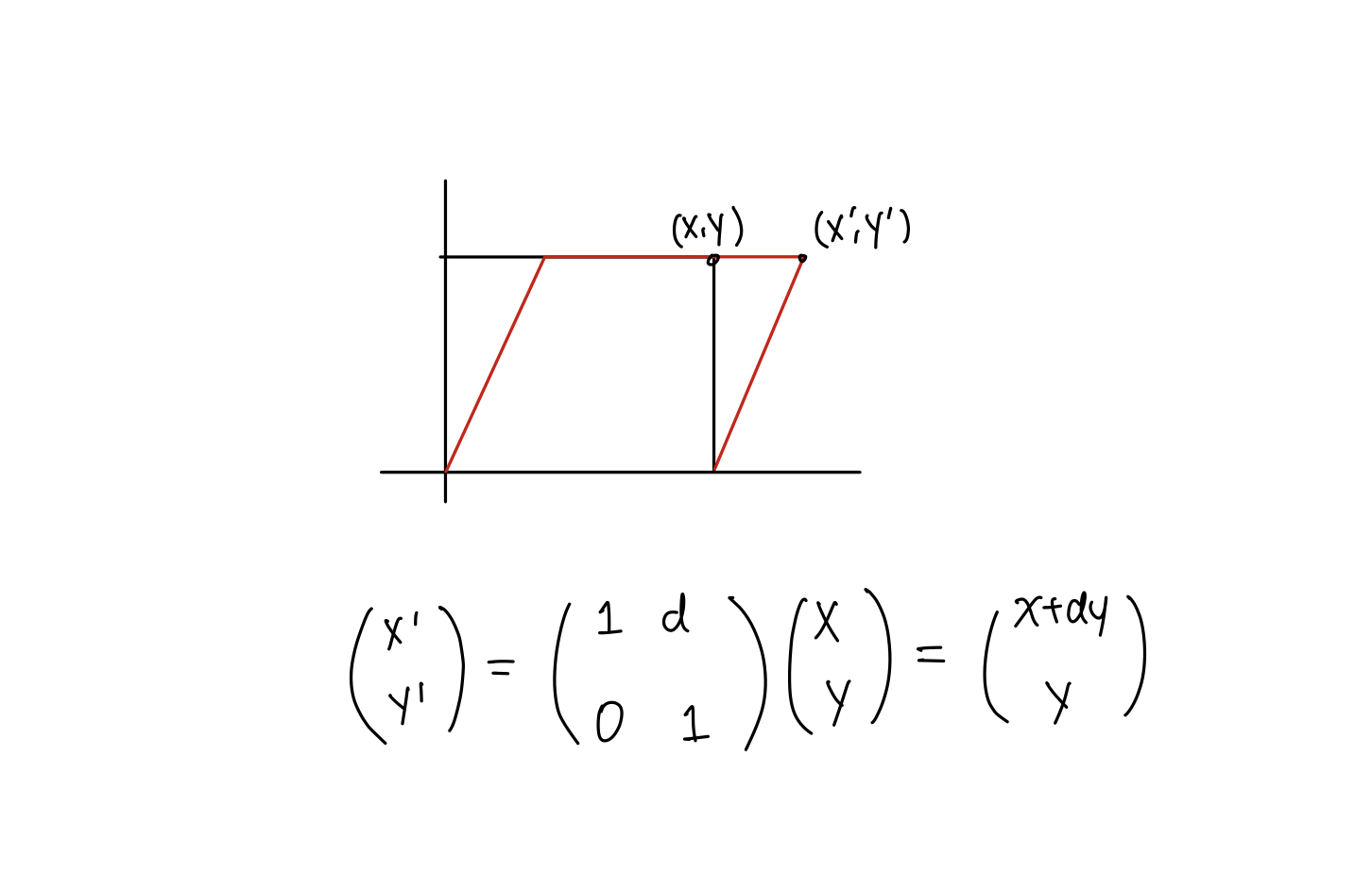
2D translation

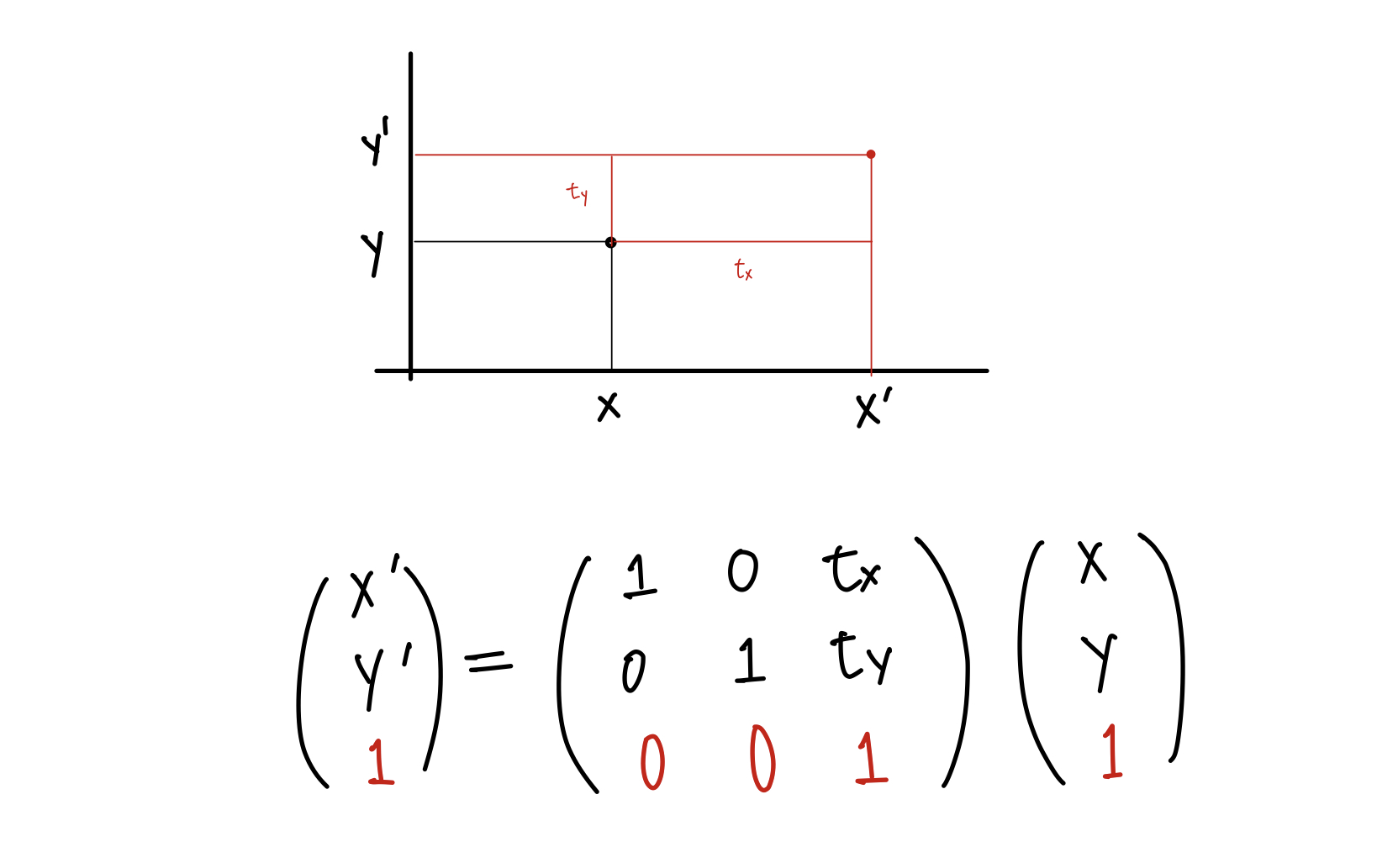
점의 이동(translation)은 동차 좌표계를 도입하여 선형변환으로 표현할수 있다. (점의 이동 자체는 선형변환이 아니다.)

Homogeneous Coordinate

표현하고자 하는 점의 차원을 한 단계 높여 표현한다. 동차 좌표계의 점은 벡터 또는 점을 의미한다.

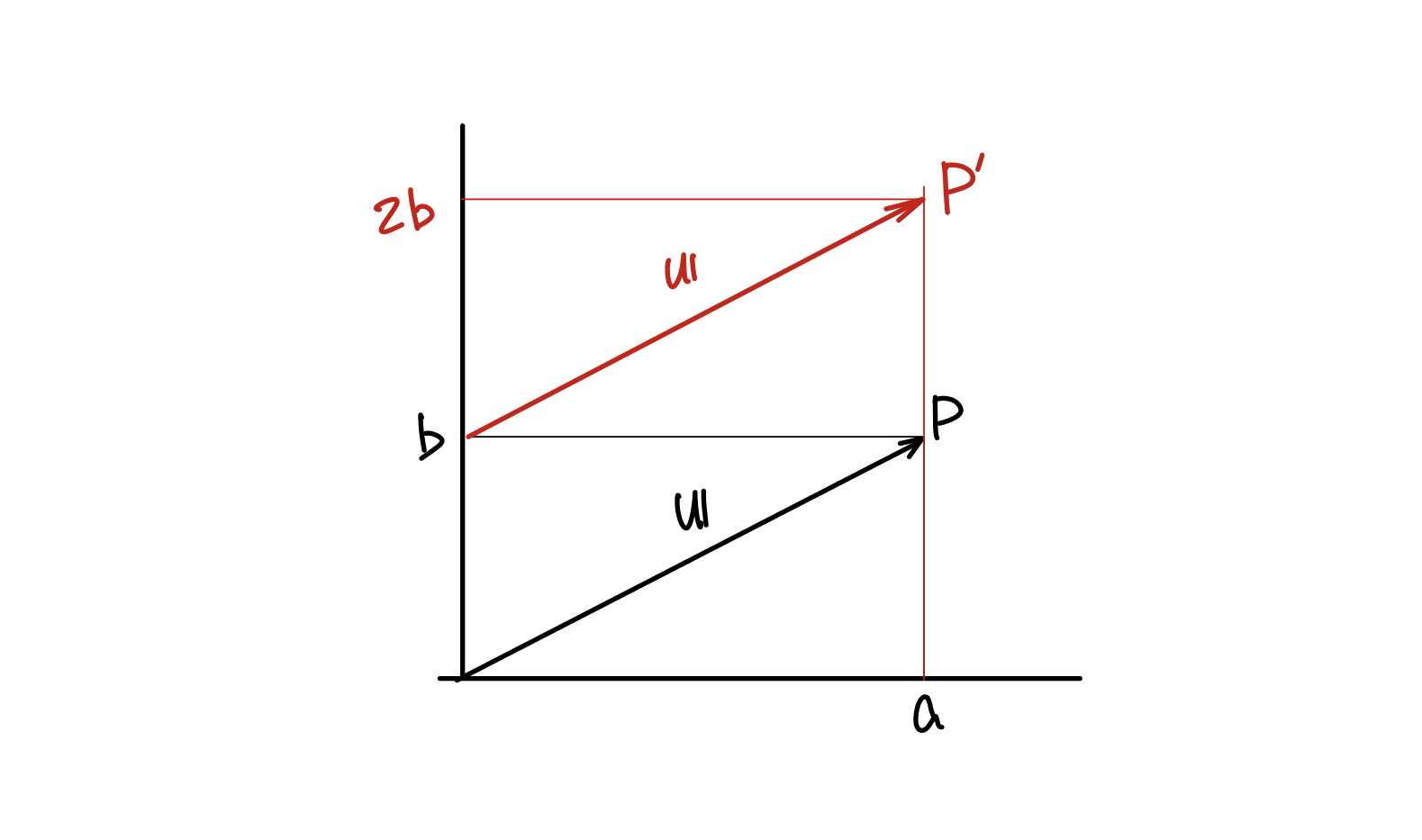
다음과 같은 2차원 평면 위에 벡터 𝐮와 점P가 존재할때, 점P를 (0, b)만큼 이동하면 새로운 점P’이 되지만 벡터𝐮는 (0, b)만큼 이동하여도 그대로 벡터𝐮이다. 즉 ‘(0, b)만큼 이동’이라는 똑같은 변환을 적용했지만 결과가 다르다. 동차 좌표계를 도입하면 점과 벡터를 하나의 공간에서 계산할수 있다. 점은 (a, 2b)가 되지만 벡터는 그대로 (a, b)이다.
2차원의 점과 벡터 (x, y)는 모두 동차좌표계에서 (x, y, w)로 표현된다. w=0인 점은 벡터, w=1인 점은 점을 의미한다.

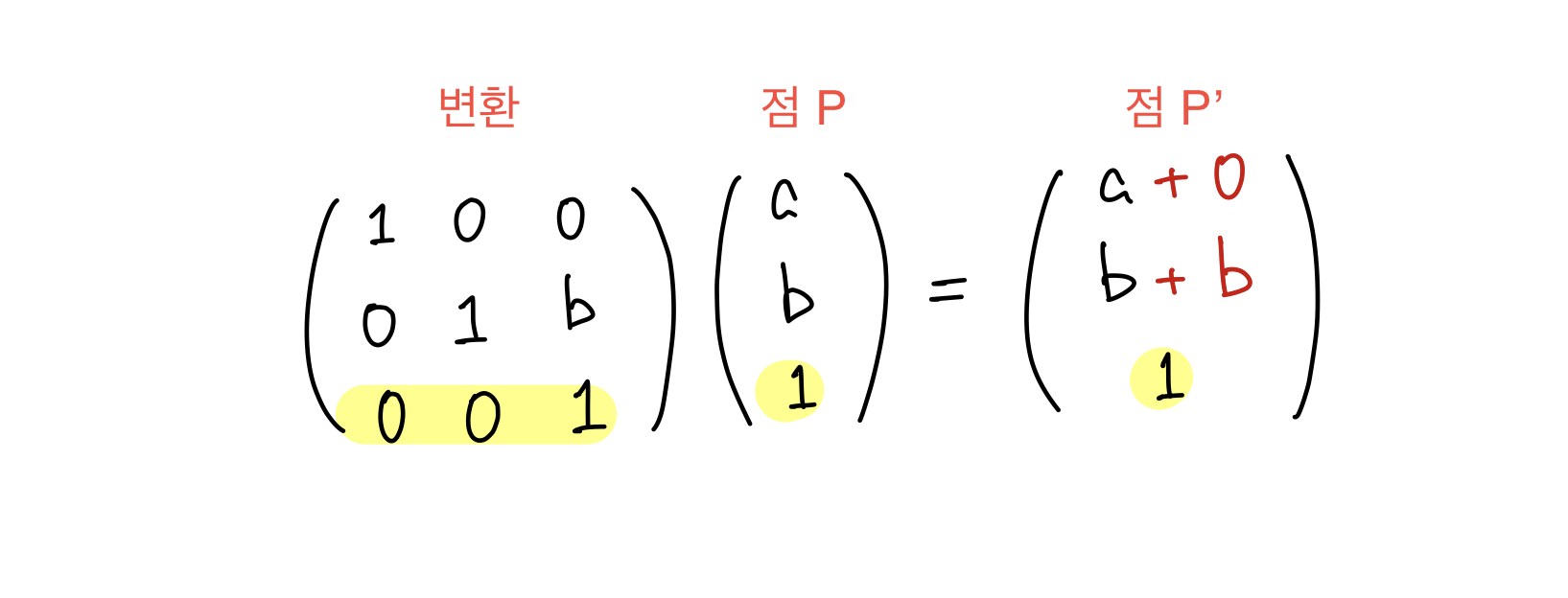
동차 좌표계에서 점P의 이동은 다음과 같은 변환(transformation)으로 표현된다.

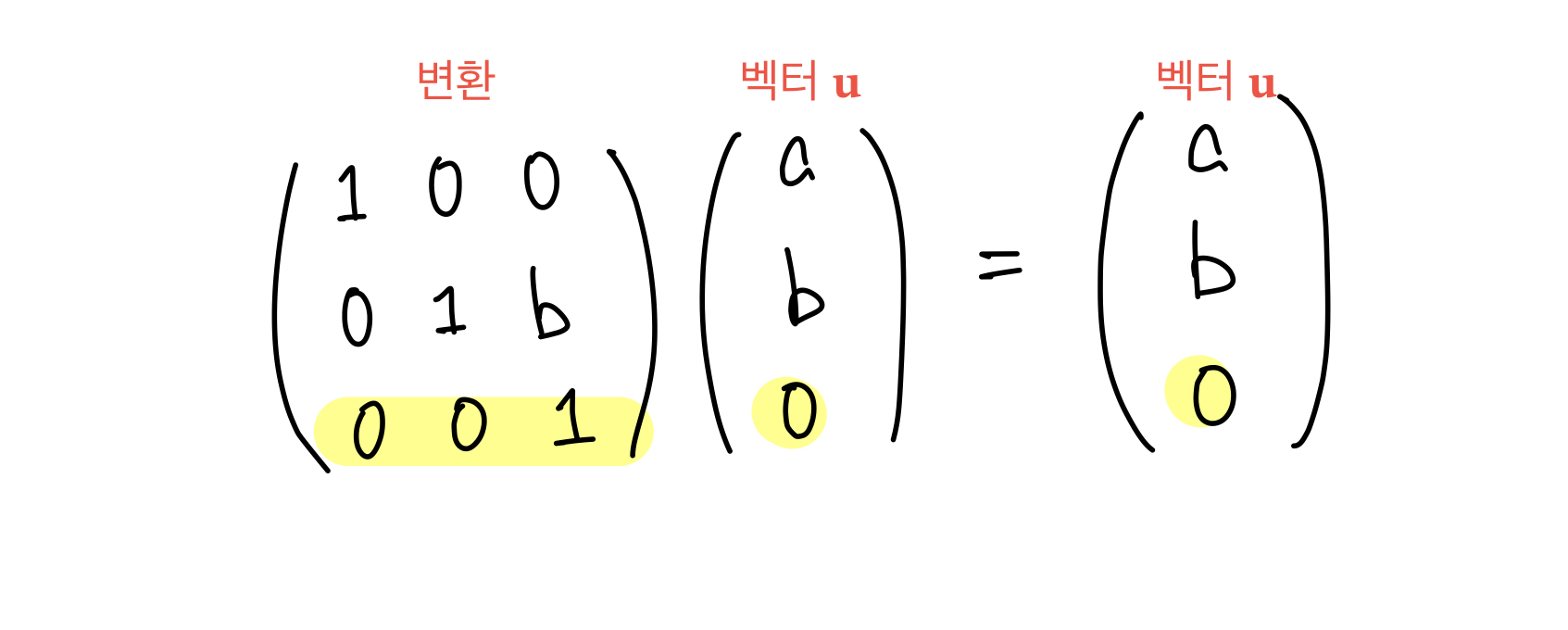
동차 좌표계에서 벡터𝘂 이동은 다음과 같은 변환(transformation)으로 표현된다.

3차원의 점과 벡터는 (x, y, z, w)로 표현되고 동일한 방법으로 변환된다.

Compound Transformation

일련의 변환들을 하나의 행렬로 표현할수 있다.

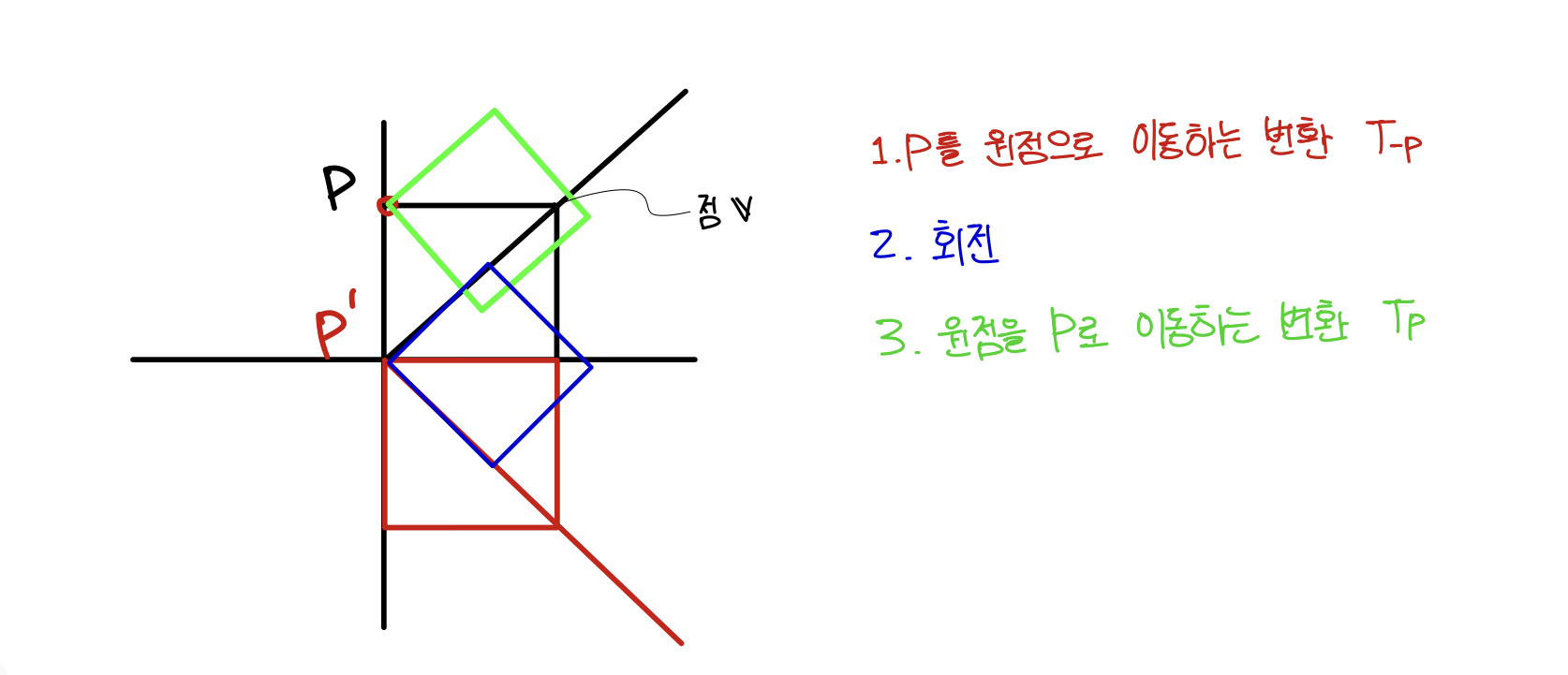
예를 들어 점v가 “점 P에 대해 θ만큼 회전” 하는 과정은 다음과 같다.

(점 P를 원점으로 이동하는 변환) -> (회전 변환) -> (원점을 점 P로 이동하는 변환)

변환을 다음과 같이 행렬의 곱으로 표현할수 있다.

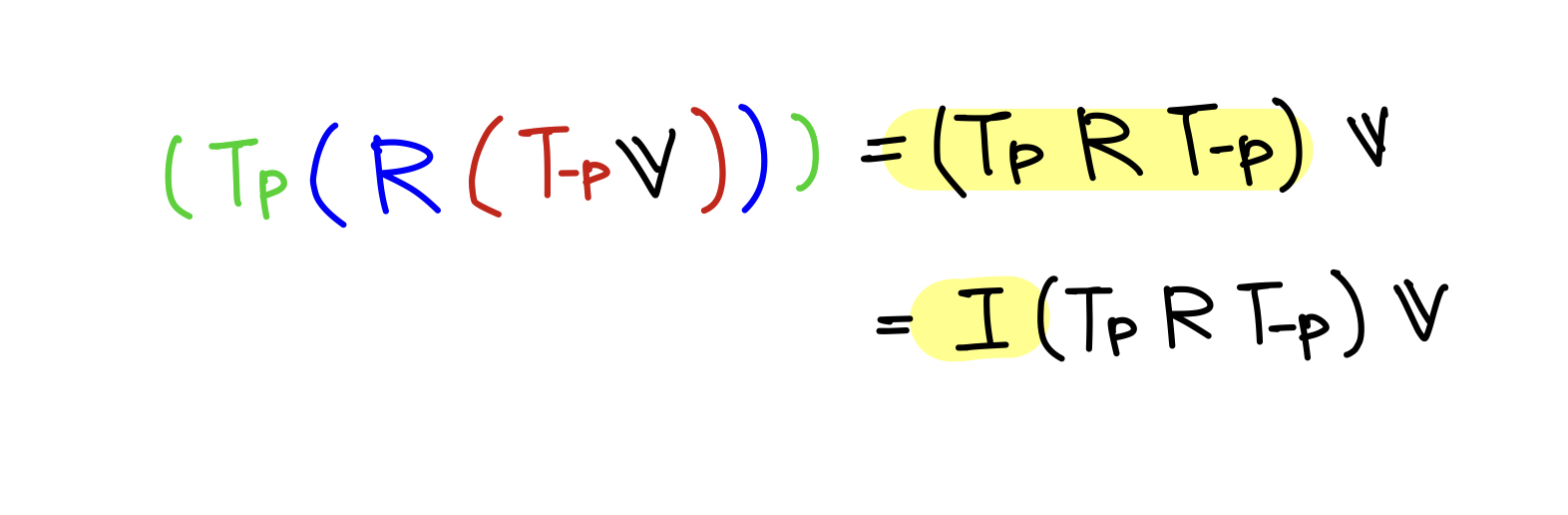
위의 식은 두 가지 방식으로 해석이 가능하다.

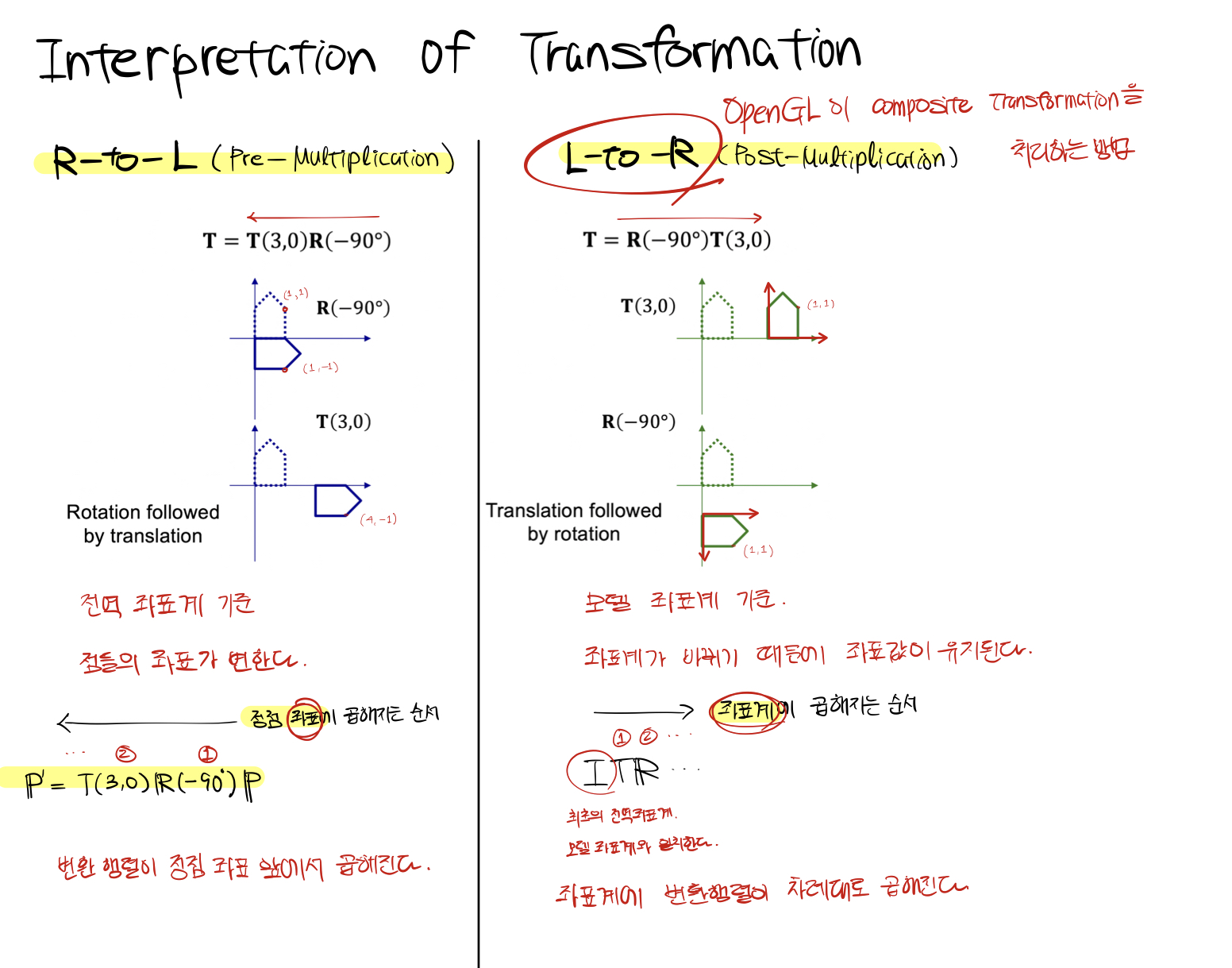
L-to-R(post-multiplication)

일련의 변환을 좌표계(frame)에 적용한다고 해석한다.
이 식의 맨 앞의 항등행렬 I는 2차원 직교좌표계의 basis (𝐞1(x축), 𝐞2(y축))라고 생각할수 있다. 즉 아래와 같이 좌표계 자체에 변환을 적용한다고 해석할수 있다.
(좌표계를 P로 이동) -> (좌표계를 회전) -> (좌표계를 원점으로 이동)

변환된 좌표계는 전역 좌표계(WCS)에서 분리된 지역 좌표계(LCS)이다.

점이 아닌 좌표계에 변환을 적용하기 때문에 점의 좌표값은 변하지 않는다.
변환이 끝난 좌표계에 점(열 벡터)을 곱하면 전역 좌표계 상에서의 위치를 계산할수 있다. 그렇기 때문에 점이 포함된 좌표계 행렬을 가지고 있어야 한다.

R-to-L(pre-multiplication)

일련의 변환을 점에 대해 적용한다고 해석하는 방식이다.

점의 좌표가 변한다.

Pivot-Point Rotation

임의의 점을 중심으로 회전하는 변환

Fixed-Point Scaling

특정 점을 기준으로 scaling

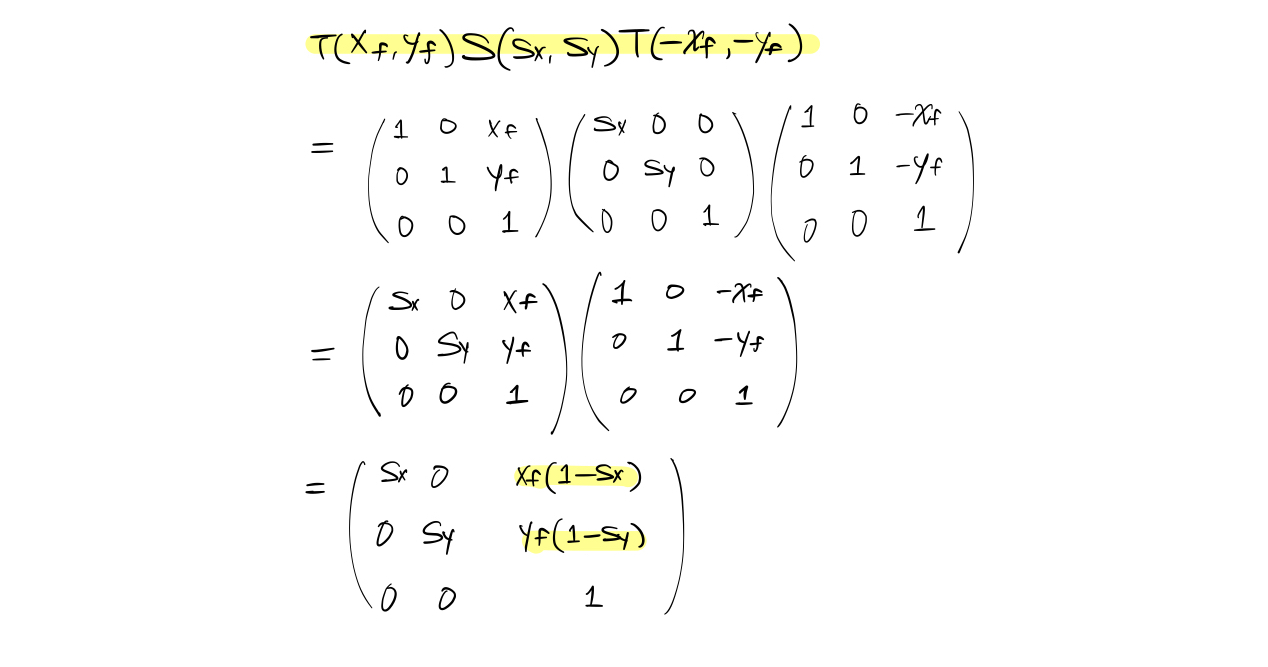
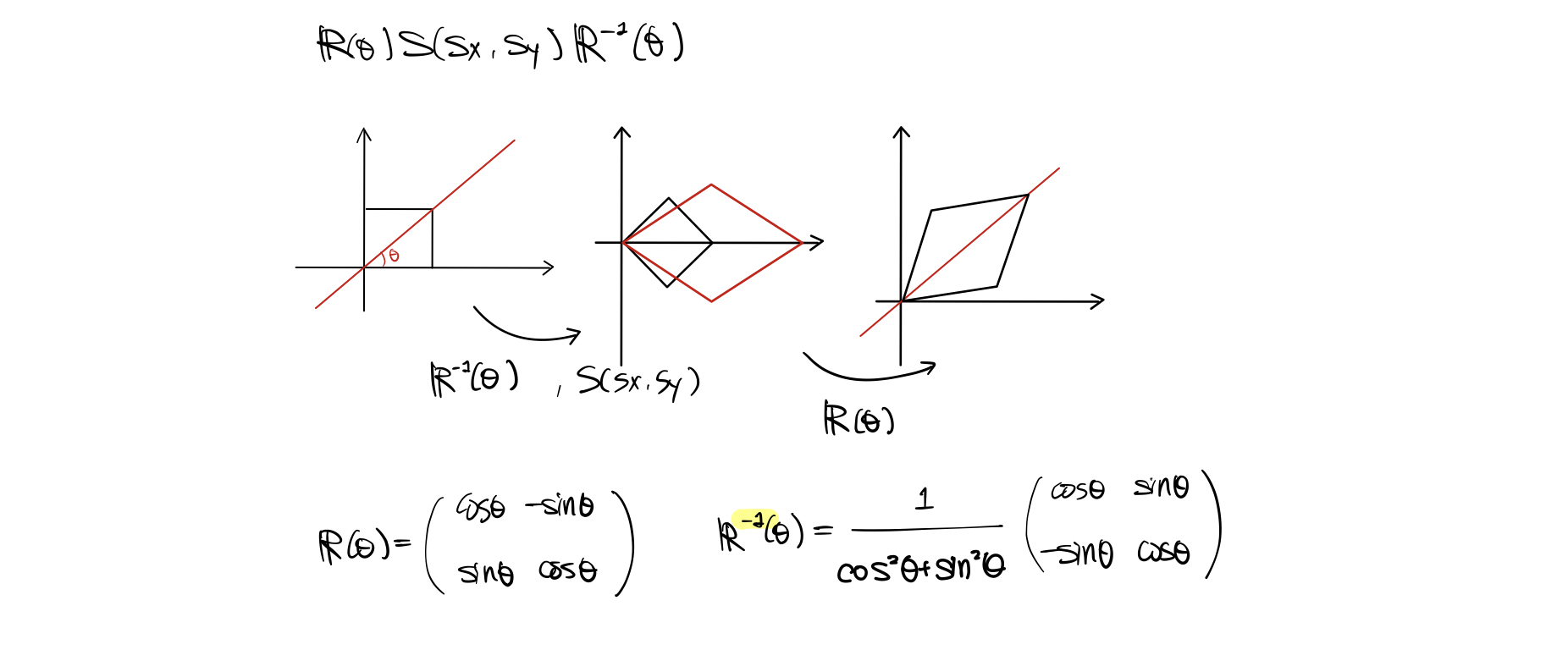
Directional-Scaling

임의의 축을 따라 scaling

Euler angles for 3D rotations

Euler angle이란 3차원 고정 좌표계에 놓인 강체(rigid body)의 방향을 표현하기 위해 도입한 세 개의 각도이다. 3차원 좌표계에서의 방향을 표현하는 다른 방식에는 고정 각도 표현법이 있다. 고정 각도 표현법에서는 두 개의 각도(고도각과 방위각)를 이용하여 방향을 표현한다. 오일러 각도는 회저한 축을 기준으로 다음 회전이 진행된다.

XYZ, ZXY, ZXZ, XYX, YXY, YZY, ZYZ, ZXZ, XZY, YXZ, YZX, ZYX와 같이 12가지 방법으로 표현이 가능하다. 오일러 각도에 의한 회전은 순서가 다르면 그 결과가 다르다. 일반적으로 ZYX가 널리 사용된다.

오일러 각도로 표현된 방향은 아래와 같이 하나의 행렬로 표현할수 있다.

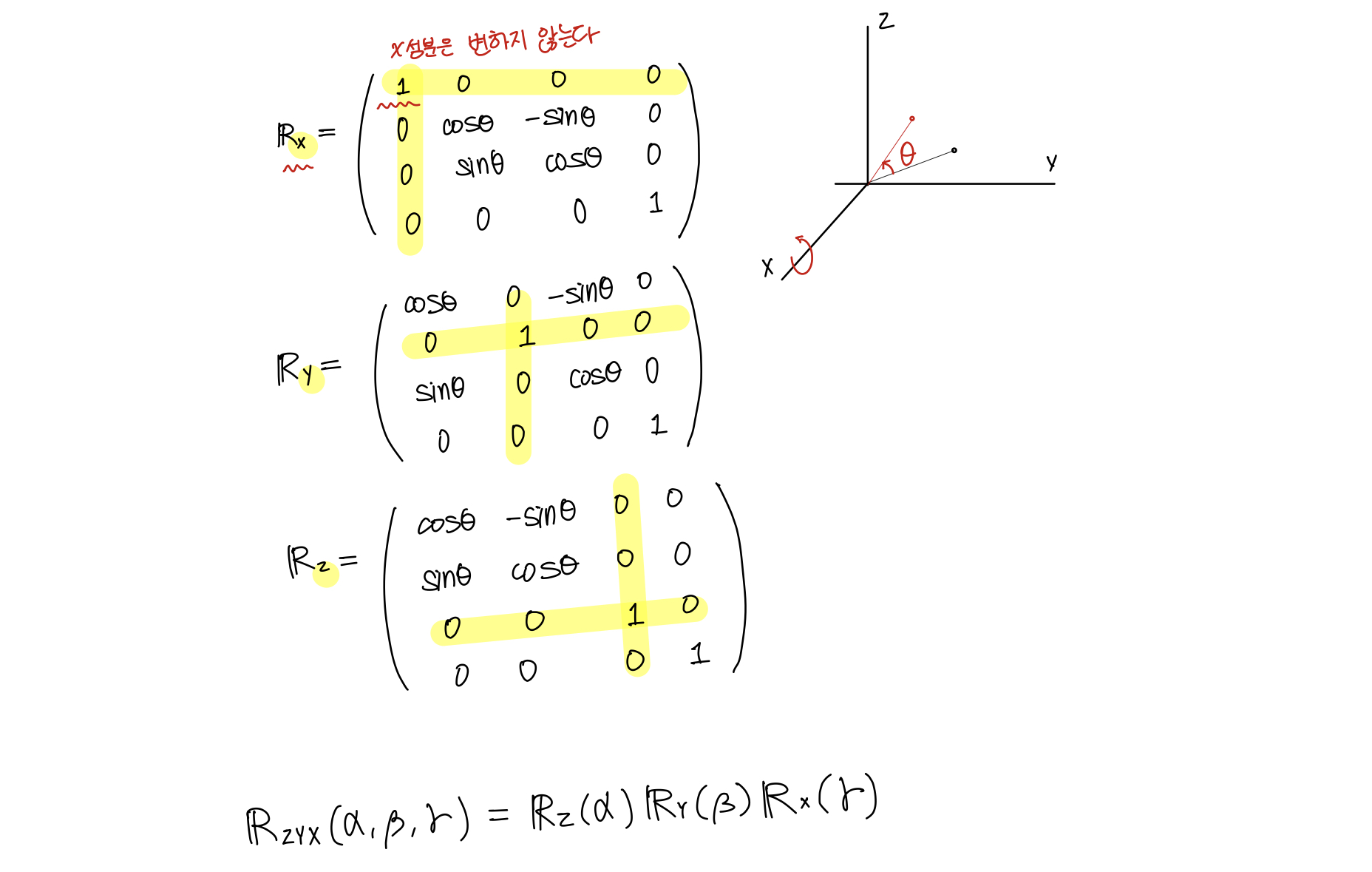
Rodrigues’ formula

임의의 축 𝐯를 중심으로 임의의 각도 𝑎만큼 회전하는 변환 행렬을 만든다.

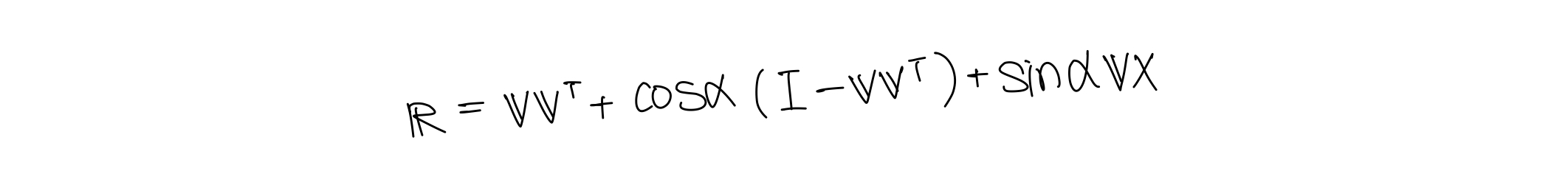
dual matrix for product

벡터의 외적을 행렬과 벡터의 곱으로 표현하기 위한 방법이다.
두 벡터 𝐯 = (v1, v2, v3), 𝐚 = (a1, a2, a3)의 외적 𝐯 x 𝐚 는 (𝐯x) 𝐚 와 같다.

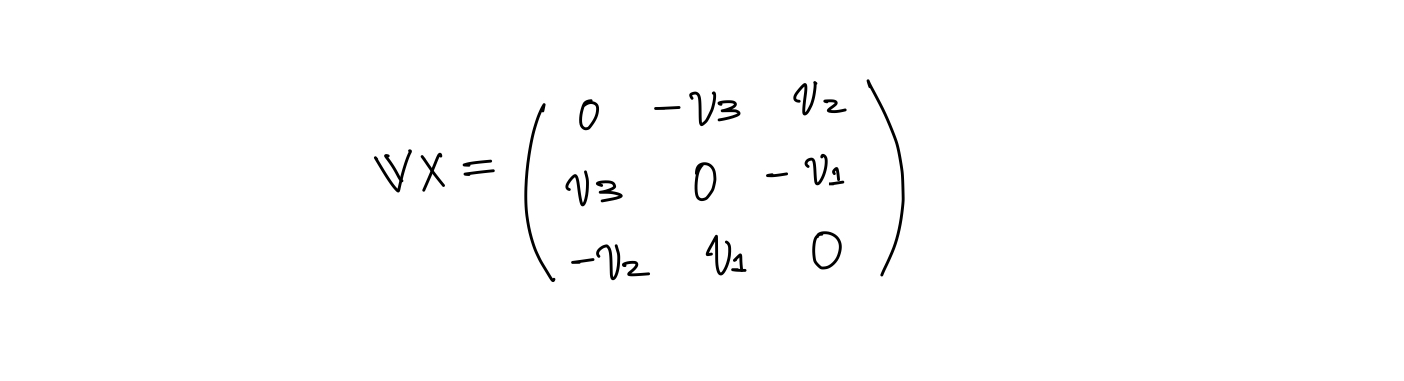
reference

• 3학년 2학기 컴퓨터그래픽스
• https://edward0im.github.io/engineering/2019/11/12/euler-angle/