순열과 조합

알고리즘 공부

순열

1부터 n까지의 수 중에서 r개를 뽑아 줄을 세우는 경우를 출력한다.

중복을 피하기 위한 기록 (used,usedIndices)이 필요하다.

Python3 코드

#! /usr/bin/env python3

n, r = map(int, input().split())
num = [(i+1) for i in range(n)]

answer = []
used = [False] * (n+1)
def permutation():
    if len(answer) == r:
        print(answer)
        return
    else:
        for n in num:
            if not used[n]:
                answer.append(n)
                used[n] = True
                combination()
                answer.pop()
                used[n] = False
            else:
                continue

permutation()

Java 코드

private static List<List<Integer>> permutation(List<Integer> numbers, int r) {
    List<Integer> tmp = new ArrayList<>(r);
    List<List<Integer>> results = new ArrayList<>();
    List<Integer> usedIndices = new ArrayList<>(numbers.size());
    permutationDFS(numbers, tmp, results, usedIndices, r);
    return results;
}

private static void permutationDFS(List<Integer> numbers, List<Integer> tmp,
    List<List<Integer>> results, List<Integer> usedIndices, int r) {
    if (tmp.size() == r) {
        results.add(new ArrayList<Integer>(tmp));
    } else {
        for (int i = 0; i < numbers.size(); i++) {
            if (!usedIndices.contains(i)) {
                tmp.add(numbers.get(i));
                usedIndices.add(i);
                permutationDFS(numbers, tmp, results, usedIndices, r);
                tmp.remove(tmp.size() - 1);
                usedIndices.remove(usedIndices.size() - 1);
            }
        }
    }
}

조합

1부터 n까지의 수 중에서 r개를 뽑는 경우를 출력한다.

순열과 다르게 뽑은 순서를 고려하지 않는다. 예를 들어 [1,2,3]과 [3,1,2]는 같은 경우이므로 둘 중 하나만 출력해야 한다.

Python3 코드

#! /usr/bin/env python3

n, r = map(int, input().split())
num = [(i+1) for i in range(n)]

answer = []
def combination(index):
    if len(answer) == r:
        print(answer)
        return
    else:
		# 순열과 달라진 부분
        for i in range(index, n):
			answer.append(num[i])
			combination(i+1)
			answer.pop()

combination(0)

• index : 이전에 조합에 포함한 원소를 다시 포함하지 않기 위해 추가된 매개변수.
  새로 조합에 추가할 숫자를 num[index]부터 찾는다.
• used 는 필요 없다.

Java 코드

private static List<List<Integer>> combination(List<Integer> numbers, int r) {
    List<Integer> tmp = new ArrayList<>(r);
    List<List<Integer>> results = new ArrayList<>();
    combinationDFS(numbers, tmp, results, r, 0);
    return results;
}

private static void combinationDFS(List<Integer> numbers, List<Integer> tmp,
    List<List<Integer>> results, int r, int idx) {
    if (tmp.size() == r) {
        results.add(new ArrayList<Integer>(tmp));
    } else {
        for (int i = idx; i < numbers.size(); i++) {
            tmp.add(numbers.get(i));
            combinationDFS(numbers, tmp, results, r, i+1);
            tmp.remove(tmp.size() - 1);
        }
    }
}

시간 제한

재귀함수의 시간복잡도를 수식으로 표현하기는 힘들기 때문에 걸리는 시간을 측정해보았다.
C(n, r)은 r=int(n/2)일때 값이 가장 커지기 때문에 r=int(n/2)로 고정시키고 n을 변화시키며 시간을 측정했다.

#! /usr/bin/env python
import time 

n = int(input())
num = [i+1 for i in range(n)]

node = 0
arr = []
def comb(index):
    global n
    global num
    global node
    global arr
    node +=1
    if len(arr) == int(n/2):
        return
    else:
        for i in range(index, n):
            arr.append(num[i])
            comb(i+1)
            arr.pop()

start = time.time()
comb(0)
end = time.time()
print('걸린 시간: {0:5f}ms'.format((end-start)*1000))
print('탐색한 노드 수: {0}'.format(node))

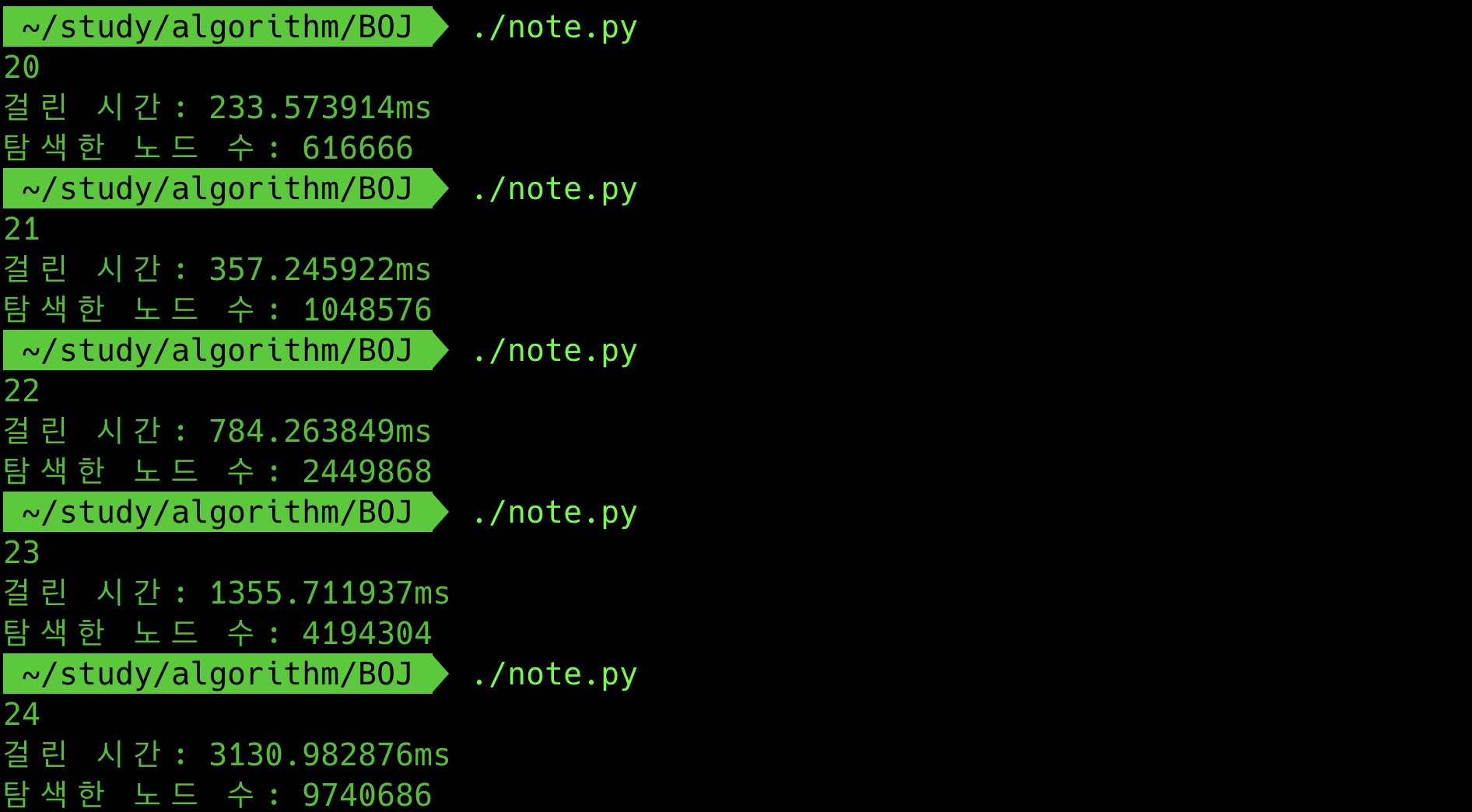
C(n,r)의 모든 조합을 생성하는데 걸리는 시간은 n=23일때 최대 1356ms이다.