프로그래머스 12936# 줄 서는 방법

알고리즘 공부

문제 보기

logic

1. 맨 앞의 숫자

입력의 크기(n)가 최대 20이기 때문에 DFS 방식으로 모든 순열을 만든 뒤 탐색하는 방식은 적절하지 않다.
(11! = 39916800)

1부터 n까지의 n개의 정수를 모두 사용하여 만들 수 있는 모든 순열을 사전순으로 나열해보자.

n = 4 일때는 다음과 같다.

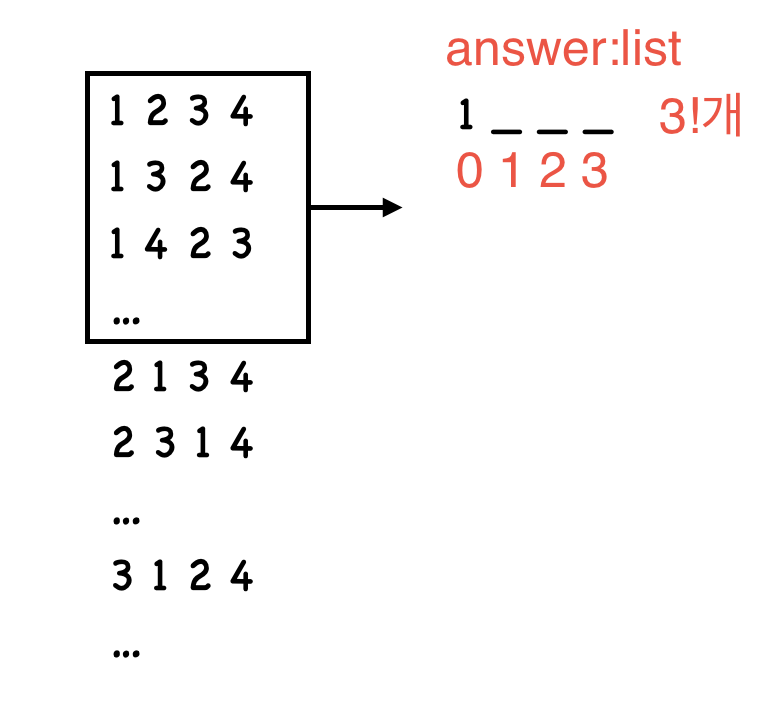
1이 가장 앞에 위치하는 순열들은 (n-i-1)!개 존재한다. (i는 리스트 answer의 index값)
마찬가지로 2, 3, 4가 가장 앞에 존재하는 순열도 똑같이 3!개 존재한다.
즉, n개의 숫자를 모두 사용하여 사전순으로 나열한 순열들은 맨 앞자리의 숫자에 대해 n개의 덩어리(동치류)으로 나뉜다.

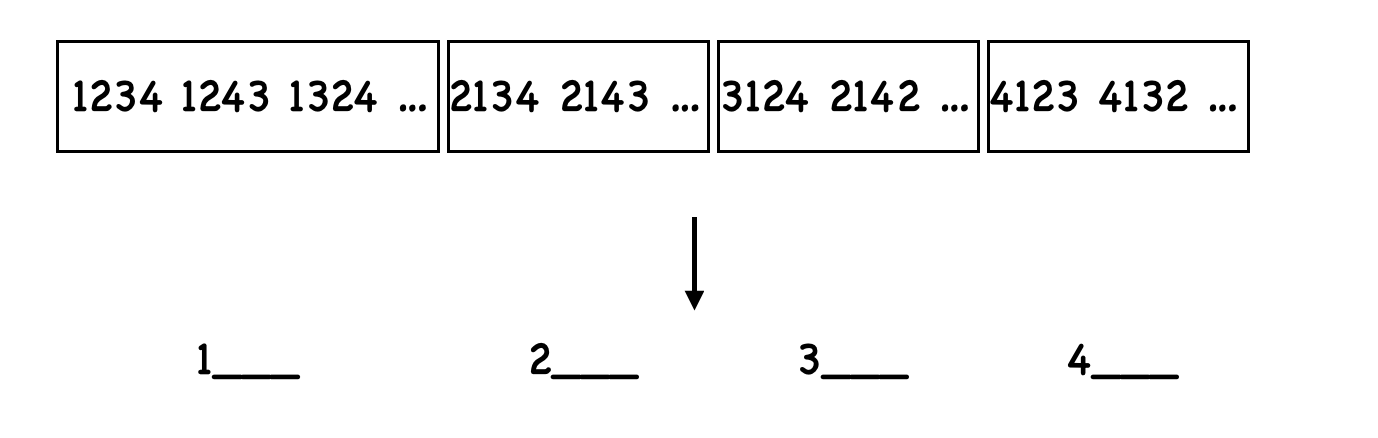
맨 앞의 숫자는 k가 몇 번째 덩어리에 포함되는지 구하면 알 수 있다.

2. 두 번째 숫자

위의 상태에서 두 번째 숫자를 추가해보자.
1은 이미 사용했기 때문에 사용할 수 있는 숫자(numbers)는 2, 3, 4 뿐이다.
이미 배열된 1을 제외한다면 2가 맨 앞에 위치하는 순열은 (n-i-1)개 존재한다.

두 번째 숫자는 k가 첫 번째 숫자로 결정된 덩어리에서 몇 번째 집합에 포함되는지 구하면 알 수 있다.

3. 일반화

answer[i]의 값 x가 결정되는 과정

• i=1: k가 전체 순열에서 몇 번째 덩어리에 포함되는지 구하면 알 수 있다.

• i=2: k가 i=1에서 구한 덩어리서 몇 번째 덩어리에 포함되는지 구하면 알 수 있다.

  …

• i=j: k가 i=j-1에서 구한 덩어리에서 몇 번째 덩어리에 포함되는지 구하면 알 수 있다.

각 단계에서 k의 값은 k % (n-i-1)!로 갱신된다. 결정된 덩어리 안에서의 k값이다.

정답 코드

from math import factorial
def solution(n, k):
    # 사용할 수 있는 숫자
    numbers = [i for i in range(1, n+1)]
    answer = []
    k = k - 1
    # answer[i]를 계산
    for i in range(n):
        # 마지막 원소는 남은 숫자
        if i == n - 1:
            x = numbers[0]
        # k가 몇 번째 덩어리에 포함되는지 계산
        else:
            x = numbers[k//factorial(n-i-1)]
            k = k % factorial(n-i-1)
        answer.append(x)
    # 한 번 사용한 숫자는 다시 사용할 수 없다.
        numbers.remove(x)
    return answer